Halo Sobat Seratus!

Tentu sobat seratus telah mengetahui tentang luas sebuah lingkaran.

Ya! Benar luas lingkaran adalah \(L=\pi r^2\)

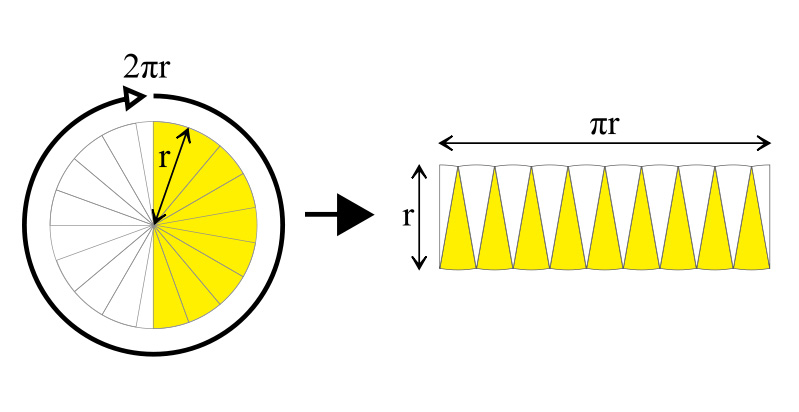
Bilangan \(\pi\) adalah sebuah konstanta Matematika yang merupakan perbandingan antara keliling sebuah lingkaran dan diameternya.

Tetapi tahukah sobat seratus? Walaupun penggunaan bilangan \(\pi\) baru disarankan oleh William Jones (1675-1740) pada tahun 1706, ternyata bilangan \(\pi\) memiliki sejarah yang panjang.

Selama ini kita tahu bahwa nilai \(\pi = \frac{22}{7}\) atau \(\pi = 3,14\). Namun sesungguhnya tidak ada satu bilangan pecahanpun yang dapat merepresentasikan nilai eksak  \(\pi\). Bahkan untuk memperoleh bilangan itu, para matematikawan telah melakukan proses pencarian yang terus menerus dan tidak kenal lelah. Pencarian bilangan  \(\pi\) ini selaras dengan pencarian perbandingan antara panjang jari-jari lingkaran dengan luasnya.   

Di Mesir, pada tahun 1800 SM terdapat catatan pada Rhind Papyrus bahwa luas lingkaran \(L=\left ( \frac{4}{3} \right )^4r^2\). Dengan demikian nilai  \(\pi\) menurut catatan itu adalah \(\pi =\left ( \frac{4}{3} \right )^4\) atau  \(\pi = 3,1605\). Sedangkan di Babilonia nilai \(\pi= \frac{25}{8} \).

Di India pada Kitab Shatapatha Brahmana disebutkan bahwa nilai \(\pi= \frac{339}{108} \) atau mendekati \(\pi= 3,1395\) . Sementara Aryabatha mengatakan, tambahkan empat dan seratus, lalu kalikan dengan delapan dan tambahkan 62000. Dengan aturan ini kita akan dapatkan keliling lingkaran dengan 20000 diameter ditemukan. Atau dengan kata lain Aryabatha mengatakan bahwa nilai \(\pi= \frac{62832}{20000} \)  atau  \(\pi= 3,1416\).

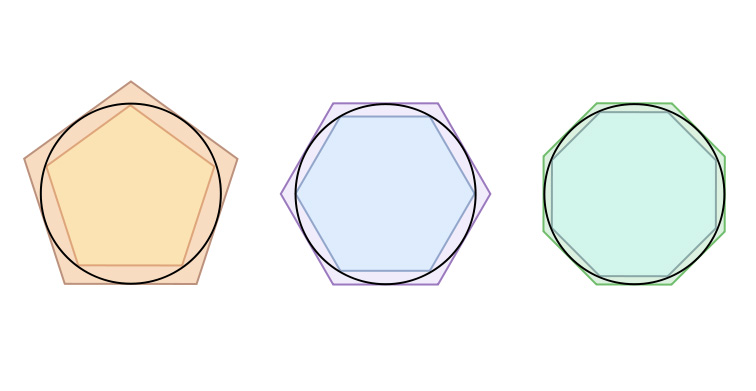
Adalah di Yunani yang juga memberikan sumbangan cukup signifikan dalam mencari nilai perbandingan antara luas lingkaran denga kuadrat jari-jari. Berawal dari Anthiphon seorang Sofis yang menyebutkan bahwa ada hubungan yang tetap antara luas lingkaran dengan kuadrat jari-jari. Anthipon lalu mencari pendekatan luas lingkaran dengan jari-jari dengan menghitung luas segibanyak beraturan dalam interior lingkaran.

Berbeda dari Anthiphon, Eudoksus mencari pendekatan luas lingkaran dengan jari-jari dengan menghitung luas segibanyak beraturan dalam interior lingkaran.

Menggabungkan ide Anthipon dengan Eudoksus, 150 tahun kemudian Archimides menyebutkan bahwa nilai  \(\pi\) berada diantara nilai pendekatan Anthipon dengan nilai pendekatan Eudoksus. Dari iterasi ini Archimedes memperoleh nilai \(\frac{223}{71}<\pi < \frac{22}{7}\). Selain itu Archimedes menetapkan bahwa luas lingkaran adalah \(L=\frac{1}{2}Kr\). Dengan K adalah keliling lingkaran dan r adalah jari-jarinya.

Nilai pendekatan yang lebih baik dari Archimedes diberikan oleh Ptolomeus dengan nilai  \(\pi = \frac{377}{120}\). Dilanjutkan oleh Liu Hui, ahli matematika dari Kerajaan Wei dengan \(\pi= \frac{3927}{1250} \) dan Zu Chongzi dari Dinasti Qi Selatan dengan  \(\pi= \frac{355}{113} \).

Pencarian terus berlanjut. Dan banyak Matematikawan yang memberikan sumbangsihnya.

Salah satu sumbangan penting tentang nilai \(\pi\) diberikan oleh Madava dari Sangamagrama(1340- 1425) dengan menyebutkan nilai \(\pi\) sebagai sebuah deret tak hingga \(\frac{1}{4}\pi = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \frac{1}{9} ....\)  yang kemudian dikenal dengan nama formula Leibniz untuk  \(\pi\). Dengan pendekatannya ini, nilai \(\pi\) akurat sampai 10 tempat desimal. Berdekatan waktunya, Jamsyid Al-Kasyi telah menentukan nilai  \(\pi\) akurat sampai 17 tempat desimal.

Matematikawa Perancis Francois Viete juga menyebutkan nilai  \(\pi\) sebagai deret tak hingga senilai \(\frac{2}{\pi} = \frac{1}{2} \sqrt{2}.\frac{1}{2}\sqrt{2+\sqrt{2}}. \frac{1}{2}\sqrt{2+\sqrt{2+\sqrt{2}}}.... \) Tetapi ini hanya akurat 9 digit saja.

Pengejaran nilai \(\pi\) masih berlanjut. Menjelang tahun 1700, Abraham Sharp, seorang matematikawan dari Inggris telah berhasil memperoleh pendekatan nilai  \(\pi\) akurat sampai 71 tempat desimal. Sedangkan John Machin juga dari Inggris justru memperoleh akurasi sampai 100 digit di belakang koma.

Adalah William Jones yang tidak ikut-ikutan mencari pendekatan nilai  \(\pi\), justru mengusulkan sebuah lambang untuk mewakili bilangan irrasional itu dengan huruf Yunani  \(\pi\).

Matematikawan lain yang tidak ikut-ikutan mencari pendekatan nilai  \(\pi\) adalah Leonard Euler dan Johan H Lambert. Eulerlah yang mempopulerkan penggunaan lambang  \(\pi\) dalam bukunya Introduction Analysis Infinitorum, selain penggunaan sigma\(\left(\Sigma \right)\) dan bilangan \(i\). Selain itu, Euler juga membuktikan bahwa  \(\pi\) kemungkinan transendent.  Sedangkan Lambert adalah orang yang pertama kali membuktikan bahwa  \(\pi\) adalah irrasional.

Namun demikian perburuan pendekatan nilai  \(\pi\) terus berlanjut. Banyak Matematikawan yang turut serta memburu pedekatan nilai \(\pi\) . Mulai dari Jurija Vega (136 dp (decimal place)), Rutherford (152 dp), Lehman (261 dp) sampai DF Ferguson di tahun 1949 (1120 dp).

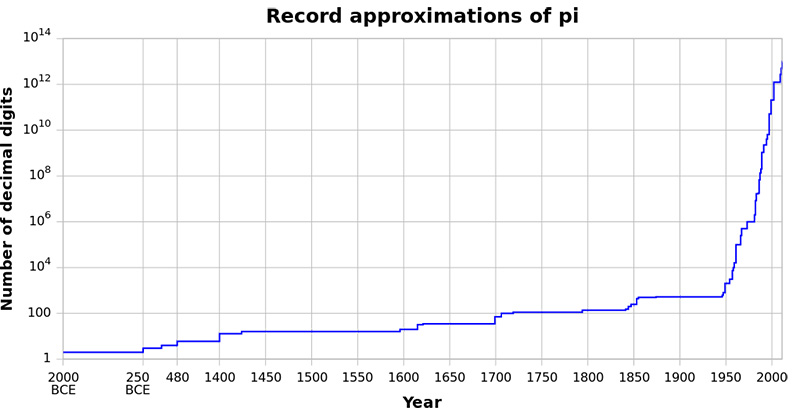
Pengejaran nilai \(\pi\)  makin akurat setelah John Wrench menggunakan Komputer yang dikenal dengan nama ENIAC (Electronic Numerical Integrator And Computer). Wrench mendapatkan nilai \(\pi\) akurat sampai 2037 tempat desimal. Setelah itu, banyak matematikawan memperoleh nilai \(\pi\) yang akurat secara signifikan dalam waktu yang cukup berdekatan. Terakhir akurasi nilai \(\pi\) sekarang sudah mencapai \(10^{13}\). Tak dapat dikesampingkan pengaruh Ramanujan yang mempublikasinya berbagai macam-macam deret pendekatan untuk \(\pi\).