Seratus Institute

OK sebelumnya telah kita bahas fungsi gelombang untuk atom. Kali ini kita akan bahas mengenai molekul diatomik.

Gambar 1. Ilustrasi molekul ion H₂⁺.

Molekul yang paling sederhana mungkin adalah molekul ion H₂⁺. Ion H₂⁺ terdiri dari dua proton dan satu elektron. Asumsikan bahwa Sobat100 dapat secara bebas menetapkan jarak antara proton.

Ketika jarak antara proton menjadi tak terhingga maka mereka tidak lagi berinteraksi. Energi keadaan dasar sistem akan menjadi - 13,6 eV, ketika elektron membentuk atom hidrogen dengan salah satu proton.

Bila jarak antar proton berada pada orde dimensi inti maka elektron akan melihat inti yang bermuatan Z = 2. Energi ikat elektron dalam keadaan dasar adalah - 54,4 eV, nilainya sama dengan energi ikat elektron dalam ion He⁺. Elektron akan terikat lebih kuat, tetapi proton juga akan saling tolak-menolak dengan kuat, sehingga energi total sistem akan positif. Karena jarak antara proton bervariasi, energi total keadaan dasar mencapai minimum untuk nilai jarak tertentu. Ini menjelaskan stabilitas molekul ion H₂⁺.

Untuk menyelesaikan masalah dengan tepat, seseorang harus menyelesaikan persamaan nilai eigen dari sistem tiga partikel. Namun, masalah dapat disederhanakan dengan menggunakan pendekatan Born-Oppenheimer . Pendekatan ini dinamai Max Born dan J. Robert Oppenheimer yang mengusulkannya pada tahun 1927, pada periode awal mekanika kuantum.^[1]

Max Born memenangkan Hadiah Nobel Fisika tahun 1954 untuk "penelitian mendasar dalam mekanika kuantum, terutama dalam interpretasi statistik fungsi gelombang".^[2] Robert Oppenheimer adalah kepala Laboratorium Los Alamos pada masa perang dan termasuk di antara mereka yang dianggap sebagai "bapak bom atom" atas peran mereka dalam Proyek Manhattan – proyek Perang Dunia II yang mengembangkan senjata nuklir pertama.^[3]

Massa elektron jauh lebih kecil daripada massa proton, oleh karena itu elektron bergerak jauh lebih cepat daripada proton. Fungsi gelombang elektronik menyesuaikan diri hampir seketika untuk setiap perubahan jarak antar-nuklir r . Pada setiap jarak antar-nuklir r , Hamiltonian yang menggambarkan gerak nuklir mengandung istilah-istilah yang terkait dengan energi kinetik inti, interaksi inti-inti, dan energi total elektron pada jarak antar-inti tersebut. Inti bergerak dalam potensial efektif

\(V_{\rm eff}(r)=E_{\rm elektron}(r)+{e^2 \over r}\ \cdots\ (1)\)  .

Untuk menemukan elektron \(E_{\rm elektron}(r)\) , persamaan nilai eigen elektron Hamiltonian, yang tunduk pada tarikan dua proton tetap, harus diselesaikan. Jarak r antara proton diperlakukan sebagai parameter, bukan sebagai variabel mekanika kuantum. Untuk molekul ion H₂⁺ persamaan nilai eigen ini dapat diselesaikan secara tepat dengan memilih koordinat yang sesuai.

Jika sumbu antar inti adalah sumbu z , maka kita telah menunjukkan bahwa L_z dan paritas adalah bilangan kuantum yang baik, tetapi L² bukanlah bilangan kuantum yang baik untuk keadaan eigen energi. ( Lihat catatan.) Untuk molekul diatomik lain dengan lebih dari satu elektron, metode pendekatan harus digunakan. Tetapi untuk semua molekul diatomik yang stabil, ditemukan bahwa memiliki magnitudo minimum pada nilai tertentu dari jarak antar-inti r .  Grafik V_eff(r) untuk molekul ion H₂⁺ ditunjukkan pada gambar di bawah ini.

Gambar 2. Tegangan Efektif molekul ion H₂⁺

Gerakan inti

Untuk molekul diatomik umum kita ingin memecahkan masalah dua inti bermassa m₁ dan m₂ dalam potensial V_eff(r). Ada derajat kebebasan vibrasi dan rotasi. Derajat kebebasan ini digabungkan. Ketika molekul bergetar, momen inersianya berubah karena jarak antar inti r berubah dan oleh karena itu energi rotasi diubah.

Mari kita pertimbangkan hanya getaran dengan amplitudo kecil .

Persamaan nilai eigen Hamiltonian untuk gerak relatif kedua inti adalah

\(\Big[-\ \frac{\hbar^2}{2\ \mu}\ \nabla^2+V(r)\Big]\phi(r)=E\ \phi(r)\ \cdots \ (2)\) ,

di mana \(\mu\) adalah massa tereduksi, \(\mu=\frac{m_1\ m_2}{m_1\ +\ m_2}\).

Jika momentum sudut inti adalah nol, maka persamaan nilai eigen direduksi menjadi persamaan radial dengan l = 0,

\(\Big[-\ \frac{\hbar^2}{2\ \mu}\ \frac{\partial^2}{\partial r^2}+V(r)\Big]u(r)=E\ u(r)\ \cdots \ (3)\).

Mari kita memperluas V(r) di sekitar posisi kesetimbangan r = r_e .

\(V(r)=-V_0+\frac{1}{2}\ V''(r_e)(r-r_e)^2+\frac{1}{6}V'''(r_e)(r-r_e)^3+\cdots\ \ \ \ \ \ \cdots (4)\).

Untuk r'= r - r_e kecil kita memiliki

\(\Big[-\ \frac{\hbar^2}{2\ \mu}\ \frac{\partial^2}{\partial r^2}+\frac{1}{2}\ V''(r_e)(r-r_e)^2\Big]u(r)\cong (E+V_0)\ u(r)\),

atau

\(\Big[-\ \frac{\hbar^2}{2\ \mu}\ \frac{\partial^2}{\partial r^2}+\frac{1}{2}\ V''(r_e)r'^2\Big]u(r')\cong (E+V_0)\ u(r')\ \cdots \ (5)\).

Ini adalah persamaan nilai eigen dari osilator harmonik satu dimensi Hamiltonian. Nilai eigennya adalah

\(E+V_0=\Big(n +\frac{1}{2}\Big)\ \hbar \ . \, \omega\ \cdots \ (6)\)

yang mana n = 0, 1, 2, dengan \(\omega^2=\) \(\frac{V''(r_e)}{\mu}\)  dan karena itu kami memiliki energi eigen dari gerakan vibrasi dari dua inti

\(E=\Big(n +\frac{1}{2}\Big)\ \hbar \ . \, \omega-V_0\ \cdots \ (7)\).

Frekuensi getaran khas berada di urutan 10¹² sampai 10¹⁴ Hz dan jatuh dalam inframerah. Fungsi gelombang keadaan dasar dari osilator harmonik memiliki penyebaran terbatas pada nilai \(\Delta r'=\) \(\sqrt{\frac{\hbar}{2\ \mu\ \omega}}\)   . ( Lihat catatan .)

Jika \(\sqrt{\frac{\hbar}{2\ \mu\ \omega}}\) << r_e, maka momen inersia hampir konstan dan untuk pendekatan yang baik maka derajat kebebasan vibrasi dan rotasi perlu dipisahkan.

Molekul heteropolar

Molekul heteropolar terdiri dari dua atom yang berbeda, contoh : HCl, CO, NO dsb. Molekul heteropolar umumnya memiliki momen dipol permanen p(r) , karena elektron tertarik lebih ke arah salah satu atom. Kita dapat memperluas p(r) sebagai fungsi jarak antar inti,

\(p(r)=p_0+p_1(r-r_e)+\ \cdots\).

Energi dari distribusi muatan yang terlokalisasi di dekat titik asal dalam medan luar diberikan oleh

\(W=q\ \phi(0)-p\ . E(0)\).

Perluasan ini menunjukkan cara karakteristik berbagai multipol dari distribusi berinteraksi dengan medan eksternal. Oleh karena itu, medan listrik berosilasi eksternal mengganggu Hamiltonian.

Keadaan eigen dari Hamiltonian terganggu dapat ditulis sebagai kombinasi linier dari keadaan eigen dari Hamiltonian tidak terganggu. Jika pada t = 0 sistem dalam keadaan | n > , maka peluang suatu saat nanti dapat ditemukan pada keadaan | n' > akan sebanding dengan | < n' | (r - r_e ) | n > |². 

Karena r - r_e = r' memiliki elemen matriks bukan nol hanya di antara keadaan yang n' = n ± 1, kita hanya mengamati penyerapan dan emisi inframerah pada satu frekuensi Bohr, \({\omega \over 2\pi}\). (Istilah urutan lebih tinggi karena ketidakharmonisitas potensi yang diamati, tetapi jauh lebih lemah.)

Molekul homopolar

Molekul homopolar terdiri dari dua atom identik, tidak aktif dalam inframerah contoh H₂. Hamiltonian untuk gerak nuklir tidak terganggu oleh medan listrik yang berosilasi, karena distribusi muatan tidak memiliki momen dipol permanen. Namun Hamiltonian untuk gerak elektronik terganggu, dan oleh karena itu molekul dapat memperoleh momen dipol terinduksi.

Jika frekuensi medan listrik berosilasi terletak pada rentang optik, transisi antara keadaan elektronik dapat diinduksi. Energi foton \(\hbar\ \Omega >>\hbar\ \omega\) dapat diserap dan dipancarkan kembali. Fenomena ini disebut hamburan Rayleigh. Jika selama penghamburan terjadi transisi antara | n > dan | n ± 1 >, maka energi foton yang dihamburkan adalah \(\hbar\ (\Omega \ \mp\ \omega)\). Oleh karena itu kita dapat mengamati foton tersebar dari tiga frekuensi yang berbeda.

• \(\hbar\ \Omega \) ( Garis Rayleigh ),
• \(\hbar\ (\Omega -\ \omega)\) ( Garis Raman-Stokes ),
• \(\hbar\ (\Omega \ +\ \omega)\) ( Garis Raman-anti Stokes ).

Ini juga dapat diamati dengan molekul heteropolar.

Sekarang mari kita mempelajari gerak rotasi molekul. Kita abaikan getaran dan menganggap bahwa jarak r antara inti tetap konstan. Kemudian gunakan rigid rotator. ( Lihat catatan ) Diperoleh

\(H=\) \(\frac{L^2}{2\ \mu\ r^2}\) \(=\) \(\frac{L^2}{2\ I}\),

dan

\(I=m_1\ {r_1}^2+m_2\ {r_2}^2=\mu\ r^2\)

Fungsi eigen dari H adalah fungsi eigen dari L² . Ini adalah harmonik bola, \(Y_{l\ m}(\theta , \phi)=<\hat{r}|l , m>\). Nilai eigennya adalah \(E_l=\) \(\frac{l\ (l+1)\ \hbar^2}{2\ I}\). Didefinisikan \(B=\) \(\frac{\hbar}{4\ \pi\ I}\), dan menulis ulang energi \(E_l=B\ h\ l\ (l+1)\). Pemisahan antara tingkat yang berdekatan adalah

\(E_l-E_{l-1}=B\ h\ [l\ (l+1)-l\ (l-1)]=2\ B\ h\ l\ \cdots\ (8)\),

itu meningkat linier dengan l. Setiap nilai eigen energi ( 2 l + 1 ) mengalami degenerasi lipat.

 
Gambar 3. Pemisahan antara tingkat yang berdekatan.

Jika sebuah molekul heteropolar dengan momen dipol p ditempatkan dalam medan listrik yang berosilasi \(\vec{E}=E\ \hat{z}\), peluang bahwa medan tersebut menginduksi transisi dari keadaan eigen rotasi | l,m > ke keadaan eigen | l',m' > sebanding dengan \(| \langle l',m'\ |p\ . E|\ l,m\rangle|^2\).

Dengan \(p\ . E\simeq p_0\ E\ \cos \theta\), elemen matriks \(\langle l',m'\ |p\ . E|\ l,m \rangle\) sebanding dengan

\(\langle l',m'\ |\cos \theta|\ l,m \rangle=\int d\Omega\ Y^*_{l'\ m'}(\theta,\phi)\ \cos \theta \ Y_{l\ m}(\theta,\phi)\).

Dengan

\(\cos \theta\ Y_{l\ m}(\theta,\phi)=\Big(\frac{l^2-m^2}{4l^2-1} \Big)^\frac{1}{2}\ \ Y_{l-1,\ m}(\theta,\phi)+\Big(\frac{(l+1)^2-m^2}{4(l+1)^2-1} \Big)^\frac{1}{2}\ \ Y_{l+1,\ m}(\theta,\phi)\)

dan

\(\int d\Omega\ Y^*_{l'\ m'}(\theta,\phi)\ \cos \theta \ Y_{l\ m}(\theta,\phi)=\delta_{l'\ l}\ \delta_{m'\ m}\)

kita peroleh

\(<l',m'\ |\cos \theta|\ l,m>=\delta_{m'\ m}\Bigg(\Big(\frac{l^2-m^2}{4l^2-1} \Big)^\frac{1}{2}\ \delta_{l'\ l-1}+\Big(\frac{(l+1)^2-m^2}{4(l+1)^2-1} \Big)^\frac{1}{2}\ \delta_{l'\ l+1}\Bigg)\ \cdots\ (9)\).

Aturan pemilihannya adalah Δm = 0 , Δl = ±1. Untuk polarisasi medan listrik sepanjang sumbu - x dan y kita temukan Δm = ±1 , Δl = ±1. Oleh karena itu, spektrum serapan dan emisi rotasi murni terdiri dari serangkaian garis yang berjarak sama. Pemisahan frekuensi antara dua garis yang berurutan adalah 2B . Spektrum rotasi murni jatuh di daerah inframerah sangat jauh atau gelombang mikro.

Molekul homopolar yang tidak memiliki momen dipol permanen tidak aktif di daerah gelombang mikro. Namun, seperti halnya getaran, rotasi molekul dapat diamati melalui efek Raman dalam hamburan cahaya yang tidak elastis oleh molekul.

Tingkat getaran - rotasi molekul diatomik

Dalam pendekatan Born-Oppenheimer kita mengasumsikan bahwa energi potensial interaksi antara dua inti hanya bergantung pada pemisahan antar inti r. Oleh karena itu, gerak relatif kedua inti dapat dijelaskan dalam bentuk gerak partikel fiktif dengan massa tereduksi m yang bergerak dalam potensial pusat. Fungsi gelombang keadaan stasioner partikel ini berbentuk \(\Psi_{n,l,m}(r,\theta,\phi)=\)  \(\frac{u_{n,l}(r)}{r}\) \(Y_{l, m}(\theta,\phi)\), dimana \(u_{n,l}(r)\) memenuhi

\(\Big[-\ \frac{\hbar^2}{2\ \mu}\ \frac{{\rm d}^2}{{\rm d} r^2}+V(r)+\frac{l\ (l+1)\ \hbar^2}{2\ \mu\ r^2}\Big]u_{n,l}(r)=E_{n,l}\ u_{n,l}(r)\ \cdots \ (10)\),

dengan

\(V_{\rm eff}=V(r)+\frac{l\ (l+1)\ \hbar^2}{2\ \mu\ r^2}\).

Untuk l = 0 kita telah memecahkan masalah untuk osilasi amplitudo kecil dan memperoleh tingkat energi vibrasi murni molekul seperti Persamaan (7),

\(E_{n,0}=\Big(n +\frac{1}{2}\Big)\ \hbar \ . \, \omega-V_0\ \cdots \ (7^*)\).

Karena l ≠ 0 kita kira-kira \(\frac{l\ (l+1)\ \hbar^2}{2\ \mu\ r^2}\)dengan \(\frac{l\ (l+1)\ \hbar^2}{2\ \mu\ {r_e}^2}\) \(=B\ h\ l\ (l+1)\). Kami berasumsi bahwa l cukup kecil sehingga \(B\ h\ l\ (l+1)<<\hbar\ \omega\). Variasi potensial sentrifugal adalah orde  \(\frac{l\ (l+1)\ \hbar^2}{ \mu\ {r_e}^3}\) \(\Delta r=2\ B\ h\ l\ (l+1)\) \(\frac{\Delta r}{r_e}\) dan diabaikan seperti halnya suku anharmonik dalam V(r) diabaikan. Maka \(u_{n,l}(r)\) memenuhi persamaan

\(\Big[-\ \frac{\hbar^2}{2\ \mu}\ \frac{{\rm d}^2}{{\rm d} r'^2}+\frac{1}{2}\ \mu\ \omega\ r'^2\Big]u_{n,l}(r')=\Big[E_{n,l}+V_0-B\ h\ l\ (l+1)\Big]\ u_{n,l}(r')\ \cdots \ (11)\),

yang lagi-lagi merupakan persamaan nilai eigen dari osilator harmonik. Oleh karena itu kita miliki

\(E_{n,l}=\Big(n +\frac{1}{2}\Big)\ \hbar \ . \, \omega-V_0+B\ h\ l\ (l+1)\ \cdots \ (12)\).

dengan n = 0, 1, 2 . . . dan l = 0, 1, 2 . . . Fungsi radial tidak bergantung pada l, karena \(-\ \frac{\hbar^2}{2\ \mu}\ \frac{{\rm d}^2}{{\rm d} r'^2}+\frac{1}{2}\ \mu\ \omega\ r'^2\) tidak bergantung pada l. Oleh karena itu, fungsi gelombang keadaan stasioner adalah \(\Psi_{n,l,m}(r,\theta,\phi)=\)  \(\frac{u_{n}(r)}{r}\) \(Y_{l, m}(\theta,\phi)\), dengan \(u_{n}(r)\) menjadi fungsi eigen osilator harmonik. Dua tingkat getaran pertama dengan struktur rotasinya ditunjukkan pada gambar di bawah ini.

 
Gambar 4. Dua tingkat getaran pertama.

Penyerapan dan emisi inframerah oleh molekul heteropolar

Jika sebuah molekul heteropolar dengan momen dipol p ditempatkan dalam medan listrik yang berosilasi \(\vec{E}=E\ \hat{z}\), peluang bahwa medan tersebut menginduksi transisi dari keadaan eigen Hamiltonian vibrasi-rotasi | n, l, m > ke keadaan eigen | n', l', m' > sebanding dengan \(| \langle n',l',m'\ |p\ . E|\ n,l,m \rangle|^2\). Dengan \(p\ . E\simeq p_0\ E\ \cos \theta+p_1\ r'\ E\ \cos \theta\), elemen matriks \(\langle l',m'\ |p\ . E|\ l,m\rangle\) sebanding dengan

.

Oleh karena itu, aturan seleksi untuk emisi dan penyerapan radiasi infra merah adalah Δl = ±1 , Δn = 0, ±1 .

Himpunan garis dengan Δn = 0 merupakan spektrum rotasi murni. Untuk Δn = ±1 nilai n' lebih besar dari dua bilangan kuantum vibrasi. Kemudian kita dapat memisahkan garis vibrasi-rotasi menjadi dua kelompok, n' = n + 1 , l' = l + 1 dan n' = n + 1 , l' = l - 1.

Untuk n' = n + 1 , l' = l + 1 frekuensi foton diberikan oleh

\({\omega \over 2\pi}+B\ (l+1)\ (l+2)-B\ (l+1)\ l={\omega \over 2\pi}+2B\ (l+1)\).

dengan l = 0, 1, 2 . . . Garis-garis di cabang R yang teramati bisa dilihat pada gambar di bawah ini.

 
Gambar 5. Garis - garis cabang P dan cabang R.

Untuk n' = n + 1 , l' = l - 1 frekuensi foton diberikan oleh

\({\omega \over 2\pi}+B\ (l'+1)\ l'-B\ (l'+2)\ (l'+1)={\omega \over 2\pi}-2B\ (l'+1)\).

dengan l' = 0, 1, 2 . . . Maka yang teramati garis-garis di cabang P. Di setiap cabang jarak antara garis yang berdekatan adalah 2B . Interval pusat yang memisahkan kedua cabang tersebut memiliki lebar 4B . Tidak ada garis pada frekuensi getaran murni \({\omega \over 2\pi}\). Spektrum getaran murni yang terdiri dari satu garis tidak ada. Tetapi dengan instrumen dengan resolusi yang buruk, kita mungkin tidak dapat menyelesaikan struktur rotasi dan memperlakukan pita yang ditunjukkan pada gambar sebagai satu garis.

Berikut ini berbagai macam spektrum untuk beberapa molekul

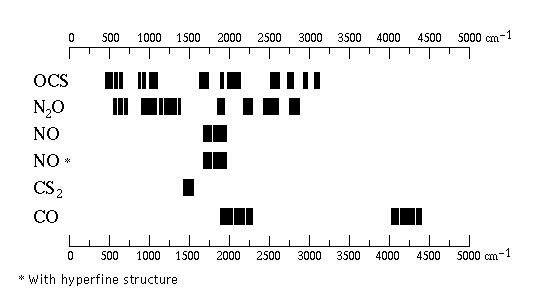
Gambar 6. Spektrum beberapa molekul ^[4]

Contoh Karbon Monoksida

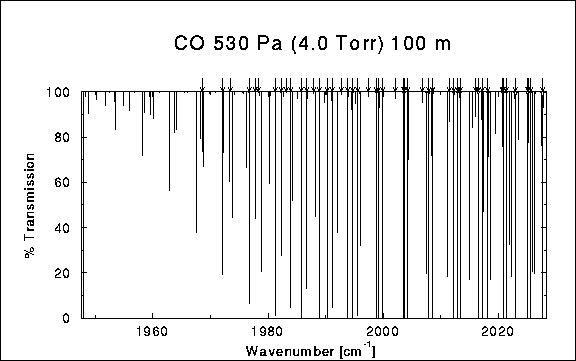
Gambar 6. Spektrum Molekul CO^[4]

DAFTAR PUSTAKA

1. ^{^} Max Born; J. Robert Oppenheimer (1927). "Zur Quantentheorie der Molekeln" [On the Quantum Theory of Molecules]. Annalen der Physik (in German). 389 (20): 457–484.
2. ^{^} The Nobel Prize in Physics 1954. The Official Web Site of the Nobel Prize. nobelprize.org
3. ^{^} Hijiya, James A. (June 2000). "The Gita of Robert Oppenheimer". Proceedings of the American Philosophical Society. 144
4. ^{a, b} NIST. 2009. Wavenumbers for Calibration of IR Spectrometers, Atlas and Wavenumber Tables. National Institute of Standards and Technology. https://www.nist.gov